Abstract

In animal nutrition, the need for determining accurate and reliable requirements is increasing to maximize animal growth and performance. A considerable amount of research has been done on amino acid requirements. However, each has a different result and it is necessary to find a single representative value describing the overall patterns of the studies. The purpose of this article is to present a method of meta-analysis used to combine the results from multiple studies.

Background

The excessive or insufficient intake of amino acid has disadvantages such as growth depression and unnecessary cost increase. For these reasons, measuring accurate and reliable requirements are crucial.

For estimating requirements, linear-plateau and curvilinear-plateau models are widely applied (Fig. 1). The basic design of a dose-response trial consist of a basal diet which is deficient in the test amino acid and a graded supplementation of the amino acid. As the amount of amino acid increases, the response (i.e. average daily gain) will gradually increase to the plateau value, at which the growth is maximized. The amino acid intake above this amount would no longer influence the growth performance and will remain constant or decrease again when reaching a critical amount depending on the amino acids. Researchers can then determine the requirement by estimating minimum supply of amino acid to reach the plateau value.

However, the requirement will typically vary across studies. Therefore, it is necessary to integrate quantitative results from multiple studies to find a single representative value. The purpose of this article is to present a method which can be used to solve this problem.

1) What is meta-analysis?

Meta-analysis is a statistcal analysis that combines the results from multiple studies. It can be performed when there are multiple studies conducted for the same purpose and with comparable methods. The results then are summarized by a single statistical model representing overall patterns that best explains the observations. By incorporating the results, researchers can obtain more accurate information from meta-analysis compared to a single study.

2) Materials and methods

Data collection

Generally, the data gathered across studies are unbalanced since the result obtained from a single study is specific to the experimental condition. Therefore, to ensure that a reasonable analysis could be carried out, the published studies should be evaluated based on predetermined inclusion and exclusion criteria. A database should then consist of studies with the same selection criteria such as publication year, experimental design, number of amino acid levels and composition of feedstuffs used in experimental diets.

Statistical models

Once the studies are collected, the linear-plateau (LP) and curvilinear-plateau (CLP) models are applied to the data. These models can be written as follows:

where Yij is the growth performance, Xij is the amino acid supply, Ai is the plateau value (i.e. maximum growth), R is the minimum amino acid value which maximizes the growth and U is a parameter to be estimated. The choice of the statistical model depends on the shape of the data. Figure 1a indicates that the rate of change between the two variables, growth and amino acid, is constant while Figure 1b indicates that it is not constant. Therefore, the type of statistical regression model used to determine the requirement may result in different dietary recommendations. Among the two different types of models, a more appropriate model in the context can be determined using Akaike Information Criteria (AIC); the model that minimizes AIC is considered more suitable. Therefore, it is possible to determine the requirement by comparing AIC of the LP model with that of CLP. Statistical analysis can be conducted using R or SAS procedures.

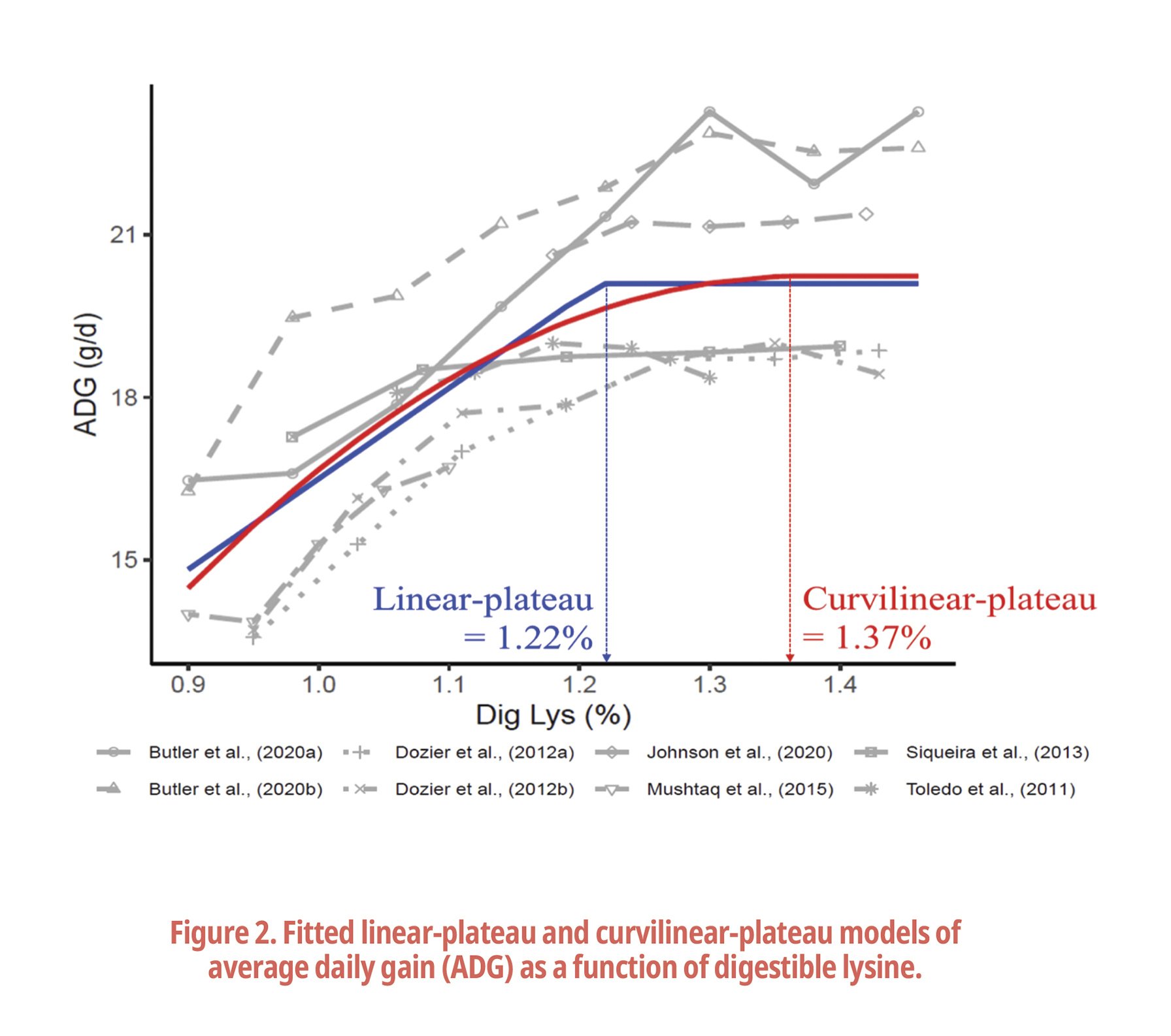
3) Example: Estimation of lysine requirement in broilers

To determine digestible lysine requirement in broilers, a database was constructed using 8 experiments based on the following selection criteria: reported after 2000, concerned broilers from 1 to 10 days and aimed to estimate digestible lysine requirement with at least three different levels of lysine. The linear-plateau (LP) and curvilinear-plateau (CLP) models were fitted to estimate lysine requirement using average daily gain as response criteria.

The estimated lysine requirements were 1.22% using the LP model and 1.37% using the CLP model (Fig. 2). The AIC obtained from these two models were 185.1 and 181.2, respectively. The AIC of the CLP model was slightly lower than that obtained from the LP model, suggesting that the CLP model fits better. Therefore, the digestible lysine can be proposed to be 1.37% according to the CLP model.

Conclusion 

Identifying accurate and reliable requirements of amino acid is essential to maximize growth performance and profitability. It is necessary to perform meta-analysis to extract quantitative results among studies since the results vary depending on the study conditions. We can estimate more accurate requirements using meta-analysis and may suggest to update the previous requirements.